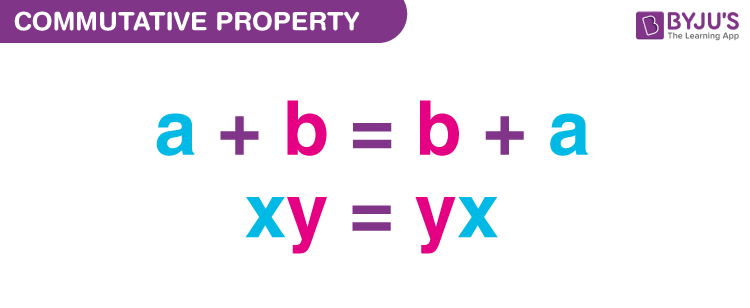In the vast realm of mathematics, the commutative property stands out as a fundamental principle that governs various operations. Have you ever considered how the order of numbers in certain mathematical expressions can alter their outcomes? If you’ve pondered this intriguing inquiry, you’re in for an enlightening journey. Let’s delve into the intricacies of the commutative property, explore its definitions, and discover captivating examples that illuminate its significance in both theoretical and practical scenarios.
The commutative property primarily applies to two fundamental arithmetic operations: addition and multiplication. In essence, this property posits that changing the order of the numbers involved in these operations does not affect the final result. Imagine your friend posed a challenge: “If I add 3 and 5, will I get the same result if I add 5 and 3?” Your instinct might be to quickly say yes, and indeed you would be correct!
To formalize this, let’s articulate the two main aspects of the commutative property:
- Commutative Property of Addition: For any two numbers a and b, the equation a + b = b + a holds true. For example, if a equals 7 and b equals 2, then 7 + 2 = 2 + 7 results in 9 in both cases.
- Commutative Property of Multiplication: For any two numbers a and b, the equation a × b = b × a also holds true. If a is 4 and b is 6, you can verify that 4 × 6 equals 24, just as 6 × 4 equals 24.
Now, imagine integrating this concept into everyday life. Suppose you are hosting a dinner party. You have seven guests arriving at 5 PM. If you invite three friends first, followed by the arrival of four colleagues, how many people are at your dinner table? Conversely, if your colleagues arrive before your friends, the total still remains unchanged. The essence of addition adapts harmoniously to the order of invitees, showcasing the delightful reliability of the commutative property.
In contrast, not all mathematical operations share this commutative charm. Take subtraction for instance. If we attempt to follow the same logic with a quick example such as 5 – 3 and 3 – 5, the results starkly diverge. The first yields 2, while the second returns -2. This disparity emphasizes that subtraction does not possess the commutative property, presenting an engaging challenge for those delving deeper into mathematical nuances.
If multiplication is also user-friendly when it comes to the commutative property, let’s explore its contribution to the efficiency of larger calculations. For instance, when multiplying two-digit numbers like 12 × 15 or 15 × 12, the order of multiplication becomes inconsequential, yet applying strategic arrangements can simplify the computational process. Just think, by rearranging terms, we can sometimes unveil hidden efficiencies!
To appreciate the commutative property fully, let’s juxtapose it against the associative property. Have you heard of this fascinating cousin of commutativity? The associative property, as it pertains to addition and multiplication, signifies that how the numbers are grouped doesn’t affect the result. For example, (2 + 3) + 4 equals 9, the same as 2 + (3 + 4). Interestingly, both properties coexist beautifully, allowing for a symbiotic relationship in problem-solving.
To further illustrate this concept, envision an algebraic expression. With variables integrated into the mix, the commutative property still reigns supreme. If we have x and y, then x + y is identical to y + x, whether you’re balancing an equation or modeling a linear relationship. Algebra thrives on such principles, and every math enthusiast must cherish these foundational precepts!
As we explore even broader applications, consider the realm of set theory. Commutative properties extend beyond mere numerical operations to larger mathematical constructs. For instance, when combining sets or unions, the order does not influence the final culmination of elements. The power of commutativity extends gracefully, enriching mathematical discourse.
In practical applications, the commutative property emerges prominently in fields ranging from computer science to economics. In algorithm design, recognizing when and how to apply the commutative property can optimize algorithms, enhancing efficiency and performance. Similarly, in finance, adding or multiplying values may yield consistent results irrespective of the sequence, allowing analysts to engage in dynamic modeling with ease.
What about the potential implications of neglecting the commutative property? As mathematics underpins so many aspects of technology and development, overlooking this essential property could lead to inaccuracies in calculations, with repercussions felt in everything from engineering designs to financial forecasts. It’s a challenge that mathematicians and practitioners alike face, emphasizing the paramount importance of understanding these foundational properties within myriad contexts.
In conclusion, the commutative property serves as a cornerstone of mathematical operations, facilitating seamless calculations and offering a sense of predictability in numerical engagements. As you think about your everyday calculations or even larger mathematical theories, remember the charm of commutativity. Whether you’re handling simple addition or complex algorithms, appreciate the order of operations and leverage this property to optimize and solve problems with finesse.
Next time someone tests your arithmetic aptitude with a playful question, reflect on the beauty of the commutative property—just like life, sometimes the order doesn’t matter, yet the sum of your understanding is undeniably profound.