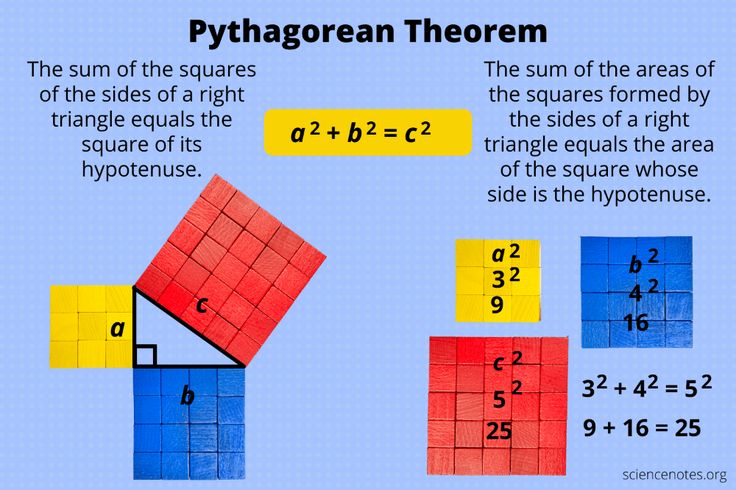
The Pythagorean Theorem stands as one of the foundational pillars of mathematics, a profound principle that has captivated minds for centuries. This theorem, attributed to the ancient Greek mathematician Pythagoras, encapsulates a simple yet powerful relationship between the sides of a right triangle. The essence of the theorem can be succinctly expressed in the algebraic equation: (a^2 + b^2 = c^2), where (c) denotes the length of the hypotenuse—the side opposite the right angle—and (a) and (b) represent the lengths of the other two sides. Herein lies an exploration of various examples that illuminate the practicality and diversity of applications for the Pythagorean Theorem.
To begin with, let’s consider a quintessential example: a right triangle with legs measuring 3 units and 4 units. The objective is to find the length of the hypotenuse. According to the theorem, we can perform the following calculations:
- First, square the lengths of the legs: (3^2 = 9) and (4^2 = 16).
- Next, sum these squares: (9 + 16 = 25).
- Finally, take the square root of the sum: (sqrt{25} = 5).
This reveals that the hypotenuse measures 5 units. Such clear-cut calculations serve as a solid introduction to the theorem, allowing students and enthusiasts to grasp the basic concepts with ease.
Beyond arithmetic, the theorem showcases its versatility in various real-world scenarios. Architects and builders, for instance, hinge their designs on the Pythagorean Theorem to ascertain the precise dimensions of structures. Imagine an architect tasked with designing a triangular roof. If one side measures 10 feet and another side measures 24 feet, the hypotenuse must be calculated to ensure stability and aesthetic appeal. Utilizing the theorem, the architect can swiftly determine, through similar calculations:
- First, calculate the squares: (10^2 = 100) and (24^2 = 576).
- Sum the results: (100 + 576 = 676).
- Next, derive the hypotenuse: (sqrt{676} = 26) feet.
Such applications highlight the theorem’s indispensable nature in the fields of construction and design, where precision is paramount.
Another compelling application arises in navigation and surveying. The theorem aids professionals in determining distances across varied terrains. Consider a scenario where a surveyor needs to calculate the shortest path between two points on a grid. If Point A is located at coordinates (1, 1) and Point B at (4, 5), the distance (hypotenuse) can be calculated using the differences in the x and y coordinates, which serve as the triangle’s legs:
- Determine the lengths of the legs: (4 – 1 = 3) and (5 – 1 = 4).
- Apply the theorem: (3^2 + 4^2 = 9 + 16 = 25).
- Thus, the distance is: (sqrt{25} = 5) units.
This example underscores the usefulness of the Pythagorean Theorem not only in abstract mathematics but also in practical applications that span various fields, including geography and transport.
Moreover, the Pythagorean Theorem can dive deeper into the fascinating realm of trigonometry. Consider deriving the height of a triangle when only the base and the length of the hypotenuse are known. Say you have a right triangle where the hypotenuse measures 10 units and the base stretches across 6 units. By employing the Pythagorean theorem, the height can be isolated:
- Calculate the square of the hypotenuse: (10^2 = 100).
- Calculate the square of the base: (6^2 = 36).
- Subtract the base’s square from the hypotenuse’s square: (100 – 36 = 64).
- Thus, the height is: (sqrt{64} = 8) units.
In this case, the Pythagorean Theorem enhances one’s understanding of spatial relationships, enabling the computation of dimensions that inform design choices and artistic expression.
Additionally, the theorem has penetrated various domains of science and technology, including computer graphics. In digital design, the theorem assists in calculating pixel distances within 2D environments, thereby facilitating object placement and movement. If a graphic designer works with an element placed at (3, 4) and needs to determine its distance from the origin (0, 0), the theorem assists in executing these calculations effortlessly:
- Calculate the distance using the coordinates: (d = sqrt{(3-0)^2 + (4-0)^2} = sqrt{9 + 16} = sqrt{25} = 5) pixels.
This demonstrates the theorem’s significance in contemporary digital artistry, where precision and accuracy are vital components of design.
In conclusion, the Pythagorean Theorem serves as a remarkable lens through which to understand both mathematical principles and their expansive applications in the real world. From architecture to navigation, and even into the domain of graphic design, the theorem exemplifies the harmony between abstract mathematics and tangible applications. The simplicity of its core equation belies the plethora of complex situations that it can elucidate. As students, professionals, and the inquisitive mind delve into the myriad examples and applications of this theorem, the profound impact of Pythagoras’ insight continues to resonate through the ages, illustrating that mathematics remains an unfathomable frontier of both practical and theoretical exploration.