Example Of An Empirical Formula

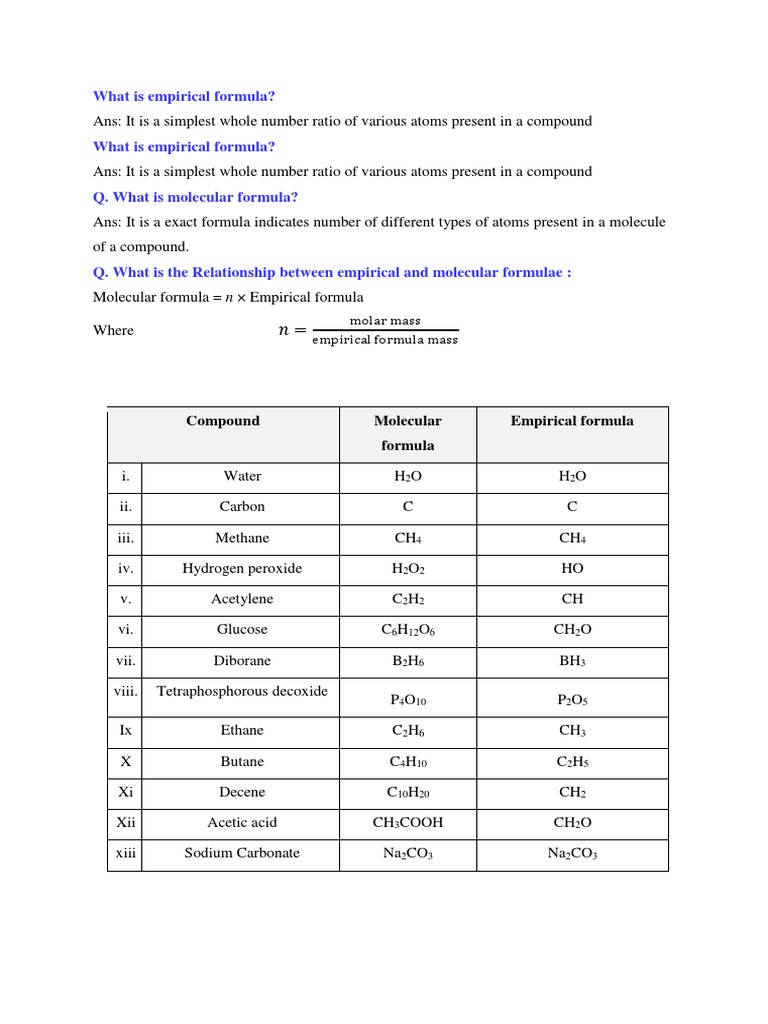
Have you ever paused to wonder what the molecular composition of the world around you looks like at the atomic level? If you have, then you’re not alone! In this exploration, we’ll delve into the fascinating realm of empirical formulas, an integral component of chemical science that succinctly denotes the simplest ratio of elements within a compound. Whether you’re a budding chemist or simply curious about the intricate dance of atoms, understanding empirical formulas can illuminate so much about chemistry’s elegant structure.

So, what exactly is an empirical formula? At its core, it serves as a shorthand representation of the specific elements that make up a compound and the relative quantities in which they exist. For instance, consider the simple molecular structure of water (H₂O). While water’s molecular formula tells us that it comprises two hydrogen atoms and one oxygen atom, the empirical formula simplifies this to its most basic ratio, which is also H₂O since the ratio of hydrogen to oxygen is already expressed in its simplest form. Isn’t it amusing how a few letters and numbers can encapsulate such vital information?

The Challenge of Balancing Ratios

Let’s pose a playful question: How well can you balance a chemical formula? Balancing the components of an empirical formula is akin to solving a puzzle where sticking to elemental integrity is crucial. The challenge often lies in taking a molecular formula, such as C₆H₁₂O₆, which represents glucose, and reducing it to the simplest integer ratio. Can you think of what the empirical formula for glucose would be? That’s right! It’s CH₂O. Here, we’ve distilled the essence of glucose down to the elemental simplicity of its components.

Types of Empirical Formulas

Empirical formulas can be classified based on their representation of elemental composition. They can exist as either whole number ratios or as fractional ratios. While whole number empirical formulas exhibit whole integers (e.g., water – H₂O), fractional ratios may arise in the case of certain compounds, exemplified by the empirical formula for benzene, C₆H₆. Although its empirical formula reduces to CH, it acknowledges the complexity of multiple structural arrangements that exist within aromatic compounds.

Moreover, these formulas extend beyond simple organic compounds. For instance, consider the empirical formula of magnesium oxide (MgO). This compound illustrates the elemental collaboration of magnesium and oxygen in a ratio that embodies the stability of ionic compounds, paving the way for numerous applications in fields ranging from construction to electrical engineering.

Applications of Empirical Formulas

The relevance of empirical formulas stretches far and wide across various scientific domains. Their utility encompasses agricultural chemistry, where they aid in understanding the nutrient compositions vital for plant growth. The precise knowledge of NPK ratios (Nitrogen, Phosphorus, Potassium) often hinges on empirical formulas, enabling farmers to optimize soil amendment strategies.

In pharmaceuticals, the accuracy of empirical formulas can mean the difference between a beneficial dosage and a harmful one. Consider the compound acetaminophen, which bears the empirical formula C₈H₉NO₂. This formula not only provides an insight into the elemental makeup but also propels the understanding of how the compound functions within the human body. The action mechanism of acetaminophen exemplifies how empirical formulas play a crucial role in medicinal chemistry.

Calculating Empirical Formulas

Calculating an empirical formula generally involves a systematic approach. To embark on this scholarly endeavor, one typically follows a series of phases. First, ascertain the mass of each element in the compound. Next, convert these masses into moles by employing the molar mass (the weight of one mole of a substance). Once this is completed, identify the simplest whole number ratio of the moles derived. The mathematical finesse involved in these calculations may seem daunting at first, but with practice, it becomes an exercise in clarity and order.

As an example, take a compound that’s composed of 40 grams of carbon and 6 grams of hydrogen. Dividing each by their respective atomic weights (approximately 12 g/mol for carbon and 1 g/mol for hydrogen), we find 3.33 moles of carbon and 6 moles of hydrogen. Upon simplification, we discover a ratio that can be expressed as C₃H₆, which is the empirical formula for propylene (an important building block in plastic manufacturing).

Limitations of Empirical Formulas